ΑΝΑΠΤΥΞΗ ΕΦΑΡΜΟΓΩΝ ΣΕ ΠΡΟΓΡΑΜΜΑΤΙΣΤΙΚΟ ΠΕΡΙΒΑΛΛΟΝ - ΠΛΗΡΟΦΟΡΙΚΗ |
|
Εκτυπώσιμη μορφή:
9o Φυλλάδιο θεωρίας - Ενότητα 1 Λίστες Δέντρα Γράφοι
|
ΠΛΗΡΟΦΟΡΙΚΗ - Ενότητα 1. Δομές Δεδομένων και Αλγόριθμοι
1. Τι ονομάζεται συνδεδεμένη λίστα;
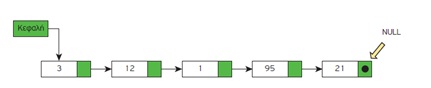
Μία (απλά) συνδεδεμένη λίστα (linked list) είναι ένα σύνολο κόμβων διατεταγμένων γραμμικά (ο ένας μετά τον άλλο).
Κάθε κόμβος περιέχει εκτός από τα δεδομένα του και έναν δείκτη που δείχνει προς τον επόμενο κόμβο.
Ο δείκτης του τελευταίου κόμβου δε δείχνει σε κάποιον κόμβο (δείκτης στο κενό).
Για να το δηλώσουμε αυτό λέμε ότι το πεδίο δείκτη του τελευταίου κόμβου έχει την τιμή NULL.
2. Πώς γίνεται η προσπέλαση σε μια συνδεδεμένη λίστα;
Για να προσπελάσουμε τους κόμβους της λίστας χρειάζεται να γνωρίζουμε τη διεύθυνση (θέση στη μνήμη) του πρώτου κόμβου της λίστας. Η διεύθυνση αυτή αποθηκεύεται σε μία ειδική μεταβλητή που την ονομάζουμε συνήθως Κεφαλή (Head).
Οι κόμβοι μιας (απλά) συνδεδεμένης λίστας είναι διατεταγμένοι σε μια συγκεκριμένη σειρά, χωρίς αυτό να σημαίνει ότι αποθηκεύονται σε συνεχόμενες θέσεις στη μνήμη. Αντίθετα, είναι διασκορπισμένοι σε όλη τη μνήμη και η σύνδεση μεταξύ τους γίνεται μέσω των δεικτών. Έχουμε άμεση πρόσβαση μόνο στον πρώτο κόμβο της λίστας. Επομένως, για να εντοπίσουμε κάποιον από τους ενδιάμεσους κόμβους, πρέπει να ξεκινήσουμε από τον πρώτο κόμβο της λίστας και να ακολουθήσουμε τους δείκτες με τη σειρά, μέχρι να φτάσουμε στον επιθυμητό κόμβο.
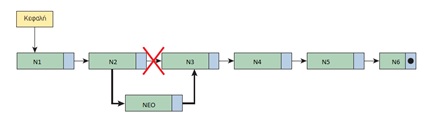
3. Πώς προσθέτω κόμβο σε μια συνδεδεμένη λίστα; Οι απαιτούμενες ενέργειες για την εισαγωγή (παρεμβολή) του νέου κόμβου είναι :
• ο δείκτης του κόμβου μετά τον οποίο θα γίνει η παρεμβολή (Ν2), να δείχνει τον νέο κόμβο (ΝΕΟ)
• και ο δείκτης του νέου κόμβου (ΝΕΟ), να δείχνει αυτό που έδειχνε ο προηγούμενος (στο Ν3) (δηλαδή, να πάρει την τιμή που είχε πριν την εισαγωγή ο δείκτης του Ν2).
Με αυτόν τον τρόπο, οι κόμβοι της λίστας διατηρούν τη λογική τους σειρά, αλλά οι φυσικές θέσεις στη μνήμη μπορεί να είναι τελείως διαφορετικές.
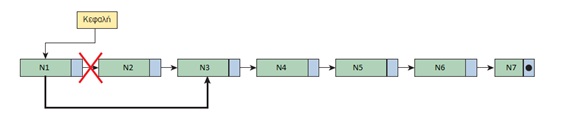
4. Πώς διαγράφω κόμβο από μια συνδεδεμένη λίστα;
Για τη διαγραφή ενός κόμβου αρκεί ν’ αλλάξει τιμή ο δείκτης του προηγούμενου κόμβου και να δείχνει πλέον στον επόμενο αυτού που διαγράφεται. Ο κόμβος που διαγράφηκε (ο δεύτερος) αποτελεί «άχρηστο δεδομένο» και ο χώρος μνήμης που καταλάμβανε, παραχωρείται για άλλη χρήση.
5. Τι είναι η διπλά συνδεδεμένη λίστα (doubly linked list); Η διπλά συνδεδεμένη λίστα είναι μια λίστα στην οποία μπορούμε να τη διατρέξουμε και προς τις δύο κατευθύνσεις.
Αυτό επιτυχάνεται με τη χρήση του δεύτερου δείκτη που δείχει τον προηγούμενο κόμβο. Προσφέρει έτσι τη δυνατότητα ξεκινώντας από οποιοδήποτε κόμβο της λίστας να μπορούμε να διατρέξουμε τη λίστα και προς τις δυο κατευθύνσεις.

6. Γιατί χρησιμοποιούνται οι συνδεδεμένες λίστες στην υλοποίηση της στοίβας και της ουράς
Οι συνδεδεμένες λίστες αξιοποιούνται για την υλοποίηση της στοίβας και της ουράς, λόγω της δυνατότητάς αυξομείωσης του μεγέθους τους.
7. Πώς μια στοίβα μπορεί να υλοποιηθεί με μία απλά συνδεδεμένη λίστα;
Οι κόμβοι (στοιχεία) εισέρχονται από την αρχή της απλά συνδεδεμένης λίστας και εξέρχονται πάλι από την αρχή της λίστας τότε ο κόμβος (στοιχείο) που εισήλθε τελευταίος εξέρχεται και πρώτος (LIFO). Επομένως η στοίβα μπορεί να υλοποιηθεί με μία απλά συνδεδεμένη λίστα αφού μπορεί να γίνει εισαγωγή κόμβου (στοιχείου) στην αρχή της λίστας και διαγραφή κόμβου (στοιχείου) από την αρχή της λίστας .
8. Πότε θα χρησιμοποιήσουμε λίστα και πότε πίνακα για την υλοποίηση μιας στοίβας;
Καλύτερη είναι η υλοποίηση στοίβας με συνδεδεμένη λίστα εκτός αν δεν γνωρίζουμε εκ των προτέρων τον μέγιστο αριθμό στοιχείων και θέλουμε μια εύκολη και γρήγορη λύση, οπότε επιλέγουμε την υλοποίηση με πίνακα.
9. Πώς μια ουρά μπορεί να υλοποιηθεί με μία διπλά συνδεδεμένη λίστα.
Στην ουρά έχουμε τις εξής δύο κύριες λειτουργίες. Εισαγωγή στοιχείου στο πίσω άκρο της ουράς και εξαγωγή στοιχείου από το εμπρός άκρο της ουράς. H ουρά μπορεί να υλοποιηθεί με μία διπλά συνδεδεμένη λίστα, αφού μπορούμε να κάνουμε εισαγωγή κόμβου στο τέλος της διπλά συνδεδεμένης λίστας. Επίσης μπορούμε να κάνουμε διαγραφή κόμβου στην αρχή της διπλά συνδεδεμένης λίστας (εξαγωγή στοιχείου από το εμπρός άκρο της ουράς).
10. Ποιες οι διαφορές ανάμεσα σε λίστες και πίνακες;
• Ο πίνακας θεωρείται μια δομή τυχαίας προσπέλασης, σε αντίθεση με μια λίστα που είναι στην ουσία μια δομή ακολουθιακής ή σειριακής προσπέλασης. Για να φθάσουμε, δηλαδή, σ’ έναν κόμβο μιας λίστας πρέπει να περάσουμε από όλους τους προηγούμενους ξεκινώντας από τον πρώτο.
• Ο πίνακας έχει σταθερό μέγεθος, το οποίο δηλώνεται εξαρχής κατά την υλοποίηση. Αυτό γίνεται, διότι ο πίνακας είναι στατική δομή δεδομένων σε αντίθεση με τη λίστα που είναι δυναμική δομή και το μέγεθός της μπορεί να μεταβάλλεται καθώς εισέρχονται νέοι κόμβοι στη λίστα ή διαγράφονται κάποιοι άλλοι.
• Oι κόμβοι της λίστας αποθηκεύονται σε μη συνεχόμενες θέσεις μνήμης σε αντιδιαστολή με τους πίνακες, όπου τα στοιχεία αποθηκεύονται σε συνεχόμενες θέσεις μνήμης.
11. Ποια είναι τα πλεονεκτήματα των λιστών (έναντι των πινάκων) ;
• Το δυναμικό τους μέγεθος,
• η ευκολία εισαγωγής και διαγραφής από οποιοδήποτε μέρος της λίστας, καθώς και
• η μη αναγκαιότητα δήλωσης του μεγέθους τους.
12. Ποια τα μειονεκτήματα των λιστών (έναντι των πινάκων);
• Η τυχαία πρόσβαση στη λίστα δεν επιτρέπεται. Είναι αδύνατο να φτάσετε στον n-οστό κόμβο μιας απλά συνδεδεμένης λίστας χωρίς πρώτα να περάσετε από όλους τους κόμβους διαδοχικά μέχρι τον συγκεκριμένο κόμβο ξεκινώντας από τον πρώτο κόμβο. Εναλλακτικά, στην περίπτωση της διπλά συνδεμένης λίστας μπορείτε να ξεκινήσετε και από τον τελευταίο κόμβο. Επομένως, δεν μπορούμε να πραγματοποιήσουμε με αποτελεσματικό τρόπο δυαδική αναζήτηση σε συνδεδεμένες λίστες.
• Οι συνδεδεμένες λίστες έχουν πολύ μεγαλύτερη επιβάρυνση από τους πίνακες, αφού οι συνδεδεμένοι κόμβοι της λίστας είναι δυναμικά κατανεμημένοι (οι οποίοι είναι λιγότερο αποτελεσματικοί στη χρήση της μνήμης) και κάθε κόμβος στη λίστα πρέπει, επιπλέον, να αποθηκεύσει έναν πρόσθετο δείκτη που θα δείχνει στον επόμενο κόμβο. Στην περίπτωση των διπλά συνδεδεμένων λιστών χρειαζόμαστε επιπλέον έναν δεύτερο δείκτη που θα δείχνει στον προηγούμενο κόμβο.
13. Ποιες είναι οι βασικές πράξεις των συνδεδεμένων λιστών;
• Εισαγωγή κόμβου στη λίστα (εισαγωγή κόμβου στην αρχή, στο τέλος της λίστας ή ενδιάμεσα).
• Διαγραφή κόμβου από τη λίστα (διαγραφή από την αρχή, το τέλος της λίστας ή ενδιάμεσα).
• Έλεγχος για το αν η λίστα είναι κενή.
• Αναζήτηση κόμβου για την εύρεση συγκεκριμένου στοιχείου.
• Διάσχιση της λίστας και προσπέλαση των στοιχείων της (π.χ. εκτύπωση των δεδομένων που περιέχονται σε όλους τους κόμβους της λίστας).
14. Τι ονομάζεται δέντρο;
Ένα δένδρο (tree) είναι μία δομή που αποτελείται από ένα σύνολο κόμβων και ένα σύνολο ακμών μεταξύ των κόμβων με βάση τους εξής κανόνες:
• Υπάρχει ένας ξεχωριστός κόμβος που ονομάζεται ρίζα. Αυτός είναι ένας κόμβος χωρίς γονέα.
• Για κάθε κόμβο c, εκτός από τη ρίζα, υπάρχει μόνο μια ακμή που καταλήγει στον κόμβο αυτόν ξεκινώντας από κάποιον άλλον κόμβο p. Ο κόμβος p ονομάζεται γονέας του c και ο κόμβος c παιδί του p.
• Για κάθε κόμβο υπάρχει μία μοναδική διαδρομή, δηλαδή, μια ακολουθία διαδοχικών ακμών, που ξεκινάει από τη ρίζα και τερματίζει σε αυτόν τον κόμβο.
Δένδρο θεωρούμε και το κενό δένδρο, δηλαδή το δένδρο που δεν έχει ούτε κόμβους, ούτε ακμές. Το κενό δένδρο είναι το μόνο δένδρο χωρίς ρίζα.

15. Σε ένα δέντρο ποιοι κόμβοι ονομάζονται φύλλα και ποιοι αδέλφια;
Οι κόμβοι χωρίς παιδιά ονομάζονται «φύλλα»
Κόμβοι με τον ίδιο γονέα ονομάζονται «αδέλφια».
16. Ποια δέντρα ονομάζονται διατεταγμένα;
Τα δέντρα στα οποία για κάθε κόμβο του υπάρχει μία γραμμική σχέση μεταξύ των παιδιών του κόμβου αυτού, αναφερόμαστε σε ένα διατεταγμένο δένδρο.

17. Σε ποιους τομείς της επιστήμης χρησιμοποιούνται τα δέντρα;
Τα δένδρα είναι μία μη-γραμμική ευέλικτη δομή δεδομένων που χρησιμοποιούνται σε πολλούς τομείς της επιστήμης των υπολογιστών, συμπεριλαμβανομένων των λειτουργικών συστημάτων, των γραφικών, των συστημάτων βάσεων δεδομένων, των παιχνιδιών, της τεχνητής νοημοσύνης και της δικτύωσης υπολογιστών.
18. Δώστε μερικά παραδείγματα χρήσης δέντρων.
• το σύστημα αρχείων του υπολογιστή
• το οικογενειακό δένδρο
• δομή ενός οργανισμού
• πίνακας περιεχομένων ενός βιβλίου
• μέρη που απαρτίζουν την μηχανή ενός αυτοκινήτου
19. Τι ονομάζεται δένδρο του παιχνιδιού (game tree);
Στα παιχνίδια ο υπολογιστής χρησιμοποιεί ένα ειδικό δένδρο, που ονομάζεται δένδρο του παιχνιδιού (game tree), το οποίο μοντελοποιεί όλες τις πιθανές κινήσεις των παικτών για να νικήσει. Κάθε κόμβος στο δένδρο, αντιπροσωπεύει μία συγκεκριμένη κατάσταση παιχνιδιού και περιέχει πληροφορίες σχετικά με το ποιος παίκτης έχει τη μεγαλύτερη πιθανότητα να κερδίσει από οποιαδήποτε πιθανή κίνηση.
20. Τι ονομάζεται δένδρο απόφασης; Δώστε παράδειγμα.
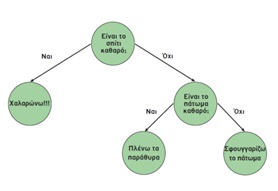
Τα δένδρα απόφασης, είναι δένδρα στα οποία :
• κάθε κόμβος αντιπροσωπεύει ένα χαρακτηριστικό (ιδιότητα),
• κάθε ακμή αντιπροσωπεύει μια απόφαση (κανόνα) και
• κάθε φύλλο αντιπροσωπεύει ένα αποτέλεσμα.
Ένα απλό πρόβλημα λήψης απόφασης μπορεί να είναι αυτό της καθαριότητας του φοιτητικού σπιτιού σας.
21. Πώς χρησιμοποιούνται τα δέντρα στον υπολογισμό αριθμητικών εκφράσεων.
Για τον υπολογισμό αριθμητικών εκφράσεων στα φύλλα του δέντρου μπαίνουν οι τελεστέοι,
ενώ στους εσωτερικούς κόμβους οι τελεστές.

22. Για ποιους λόγους τα δέντρα θεωρούνται τα τα δένδρα ισχυρές δομές.
• Ο πρώτος λόγος αναφέρεται στη δυναμικότητα των δένδρων. Είναι πολύ εύκολο να προσθέσετε, να αφαιρέσετε ή να αναζητήσετε ένα στοιχείο σε ένα δένδρο.
• Ο δεύτερος βασικός λόγος είναι ότι η δομή των δένδρων μεταφέρει πληροφορίες.
23. Τι ονομάζεται δυαδικό δέντρο;
Ένα δυαδικό δένδρο (binary tree) είναι ένα διατεταγμένο δένδρο, στο οποίο κάθε κόμβος έχει το πολύ δύο παιδιά, το αριστερό και το δεξί παιδί.
Μπορούμε, συνεπώς, να μιλάμε για αριστερό και δεξιό υποδένδρο ενός κόμβου.

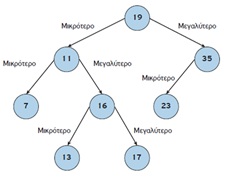
24. Τι ονομάζεται δυαδικό δέντρο αναζήτησης;
Ένα δυαδικό δένδρο αναζήτησης (binary search tree) είναι ένα δυαδικό δένδρο,
όπου για κάθε κόμβο u, όλοι οι κόμβοι του αριστερού υποδένδρου έχουν τιμές μικρότερες της τιμής του κόμβου u
και όλοι οι κόμβοι του δεξιού υποδένδρου έχουν τιμές μεγαλύτερες (ή ίσες) της τιμής του κόμβου u.
25. Τι ονομάζεται γράφος
Ένας γράφος (graph) είναι μία δομή που αποτελείται :
• από ένα σύνολο κόμβων (ή σημείων ή κορυφών)
• και ένα σύνολο γραμμών (ή ακμών ή τόξων) που ενώνουν μερικούς ή όλους τους κόμβους.

26. Ποια η συσχέτιση του γράφου με τις λίστες και τα δέντρα;
Ο γράφος αποτελεί την πιο γενική δομή δεδομένων, με την έννοια ότι όλες οι προηγούμενες δομές που παρουσιάστηκαν μπορούν να θεωρηθούν περιπτώσεις γράφων.

27. Ποιοι οι τύποι του γράφου;
• Εάν όλες οι ακμές σε έναν γράφο έχουν κατεύθυνση, ο γράφος ονομάζεται κατευθυνόμενος γράφος (directed graph).
• Εάν όλες οι ακμές σε έναν γράφο δεν έχουν κατεύθυνση, ο γράφος ονομάζεται μη κατευθυνόμενος γράφος (undirected graph) και η διαδρομή μεταξύ των δύο κόμβων είναι αμφίδρομη.



28. Τι τύπου γράφοι είναι τα κοινωνικά δίκτυα facebook, twitter και τι o παγκόσμιος ιστός;
Στον παγκόσμιος Ιστός (WWW), που είναι ένας τεράστιος γράφος,
• έχουμε κάποιες φορές ακμές που είναι :μη κατευθυνόμενες - μπορούμε να προχωρήσουμε από μια ιστοσελίδα σε μια άλλη και το αντίστροφο
• και άλλες φορές έχουμε ακμές που κατευθύνονται - μπορούμε να πάμε μόνο από την ιστοσελίδα Α στην ιστοσελίδα Β, και ποτέ το αντίστροφο.

Το Facebook είναι μη κατευθυνόμενος γράφος επειδή η σχέση μεταξύ δύο χρηστών (κόμβοι), είναι αμφίδρομη. Δεν υπάρχει η έννοια κόμβου «προέλευσης» και «προορισμού» - αντ’ αυτού, είσαι φίλος μου και είμαι δικός σου.
Το Twitter είναι κατευθυνόμενος γράφος επειδή μπορώ να σε ακολουθήσω, αλλά δεν απαιτείται να με ακολουθήσεις. Κάθε ακμή που δημιουργούμε αντιπροσωπεύει μια μονόδρομη σχέση.
• Όταν με ακολουθείς στο Twitter, δημιουργείται μια ακμή στον γράφο με τον λογαριασμό σου ως κόμβο προέλευσης και τον λογαριασμό μου ως τον κόμβο προορισμού.
• Όταν σε ακολουθώ στο Twitter, δημιουργώ μια δεύτερη ακμή, με τον λογαριασμό μου σαν κόμβο προέλευσης και τον δικό σου σαν κόμβο προορισμού
|
|
|
Για τους ακουστικούς τύπους, που ο ρυθμός μπορεί να τους βοηθήσει στην εκμάθηση της θεωρίας
η αποτύπωση της σε μελωδική μορφή. Μην χάσετε χρόνο βλέποντας τα βίντεο. Δείτε τα μόνο αν σας βοηθάνε στη μελέτη σας! Ιστοσελίδες ΑΙ που χρησιμοποιήθηκαν: https://suno.com:για δημιουργία τραγουδιών https://www.bing.com/images/create : για δημιουργίας εικόνας https://www.heygen.com/ : για δημιουργίας βίντεο 
|
|
|